Richter magnitude scale




For the American seismologist, see Charles Richter. For a review of different magnitude scales, see seismic magnitude scales.


























Part of a series on
Earthquakes











  • Earth Sciences Portal


  • Category

  • Related topics



  • v

  • t

  • e


The so-called Richter magnitude scale – more accurately, Richter's magnitude scale, or just Richter magnitude – for measuring the strength ("size") of earthquakes refers to the original "magnitude scale" developed by Charles F. Richter and presented in his landmark 1935 paper, and later revised and renamed the Local magnitude scale, denoted as "ML" or "ML". Because of various shortcomings of the ML scale most seismological authorities now use other scales, such as the moment magnitude scale (Mw ), to report earthquake magnitudes, but much of the news media still refers to these as "Richter" magnitudes. All magnitude scales retain the logarithmic character of the original, and are scaled to have roughly comparable numeric values.




Contents






  • 1 Development


  • 2 Details


  • 3 Richter magnitudes


  • 4 Magnitude empirical formulae


  • 5 See also


  • 6 Notes


  • 7 Sources


  • 8 External links





Development





Charles Francis Richter (circa 1970)


Prior to the development of the magnitude scale the only measure of an earthquake's strength or "size" was a subjective assessment of the intensity of shaking observed near the epicenter of the earthquake, categorized by various seismic intensity scales such as the Rossi-Forel scale. In 1883 John Milne surmised that the shaking of large earthquakes might generate waves detectable around the globe, and in 1899 E. Von Rehbur Paschvitz observed in Germany seismic waves attributable to an earthquake in Tokyo.[1] In the 1920s Harry O. Wood and John A. Anderson developed the Wood-Anderson seismograph, one of the first practical instruments for recording seismic waves.[2] Wood then built, under the auspices of the California Institute of Technology and the Carnegie Institute, a network of seismographs stretching across Southern California.[3] He also recruited the young and unknown Charles Richter to measure the seismograms and locate the earthquakes generating the seismic waves.[4]


In 1931 Kiyoo Wadati showed how he had measured, for several strong earthquakes in Japan, the amplitude of the shaking observed at various distances from the epicenter. He then plotted the logarithm of the amplitude against the distance, and found a series of curves that showed a rough correlation with the estimated magnitudes of the earthquakes.[5] Richter resolved some difficulties with this method,[6] then, using data collected by his colleague Beno Gutenberg, produced similar curves, confirming that they could be used to compare the relative magnitudes of different earthquakes.[7]


To produce a practical method of assigning an absolute measure of magnitude required additional developments. First, to span the wide range of possible values Richter adopted Gutenberg's suggestion of a logarithmic scale, where each step represents a tenfold increase of magnitude, similar to the magnitude scale used by astronomers for star brightness.[8] Second, he wanted a magnitude of zero to be around the limit of human perceptibility.[9] Third, he specified the Wood-Anderson seismograph as the standard instrument for producing seismograms. Magnitude was then defined as "the logarithm of the maximum trace amplitude, expressed in microns", measured at a distance of 100 km. The scale was calibrated by defining a magnitude 3 shock as one that produces (at a distance of 100 km) a maximum amplitude of 1 micron (1 µm, or 0.001 millimeters) on a seismogram recorded by a Wood-Anderson torsion seismograph.[10] Finally, Richter calculated a table of distance corrections,[11] in that for distances less than 200 kilometers[12] the attenuation is strongly affected by the structure and properties of the regional geology.[13]


When Richter presented the resulting scale in 1935 he called it (at the suggestion of Harry Wood) simply a "magnitude" scale.[14] "Richter magnitude" appears to have originated when Perry Byerly told the press that the scale was Richter's, and "should be referred to as such."[15] In 1956 Gutenberg and Richter, while still referring to "magnitude scale", labelled it "local magnitude", with the symbol ML , to distinguish it from two other scales they had developed, the surface wave magnitude (MS) and body wave magnitude (MB) scales.[16]



Details


The Richter scale was defined in 1935 for particular circumstances and instruments; the particular circumstances refer to it being defined for Southern California and "implicitly incorporates the attenuative properties of Southern California crust and mantle."[17] The particular instrument used would become saturated by strong earthquakes and unable to record high values. The scale was replaced in the 1970s by the moment magnitude scale (MMS, symbol Mw ); for earthquakes adequately measured by the Richter scale, numerical values are approximately the same. Although values measured for earthquakes now are Mw{displaystyle M_{w}}M_{w} (MMS), they are frequently reported by the press as Richter values, even for earthquakes of magnitude over 8, when the Richter scale becomes meaningless.
Anything above 5 is classified as a risk by the USGS.[citation needed]


The Richter and MMS scales measure the energy released by an earthquake; another scale, the Mercalli intensity scale, classifies earthquakes by their effects, from detectable by instruments but not noticeable, to catastrophic. The energy and effects are not necessarily strongly correlated; a shallow earthquake in a populated area with soil of certain types can be far more intense in effects than a much more energetic deep earthquake in an isolated area.


Several scales have historically been described as the "Richter scale", especially the local magnitude ML{displaystyle M_{text{L}}}M_text{L} and the surface wave Ms{displaystyle M_{text{s}}}M_{text{s}} scale. In addition, the body wave magnitude, mb{displaystyle m_{text{b}}}m_text{b}, and the moment magnitude, Mw{displaystyle M_{text{w}}}M_text{w}, abbreviated MMS, have been widely used for decades. A couple of new techniques to measure magnitude are in the development stage by seismologists.


All magnitude scales have been designed to give numerically similar results. This goal has been achieved well for ML{displaystyle M_{text{L}}}M_text{L}, Ms{displaystyle M_{text{s}}}M_{text{s}}, and Mw{displaystyle M_{text{w}}}M_text{w}.[18][19] The mb{displaystyle m_{text{b}}}m_text{b} scale gives somewhat different values than the other scales. The reason for so many different ways to measure the same thing is that at different distances, for different hypocentral depths, and for different earthquake sizes, the amplitudes of different types of elastic waves must be measured.


ML{displaystyle M_{text{L}}}M_text{L} is the scale used for the majority of earthquakes reported (tens of thousands) by local and regional seismological observatories. For large earthquakes worldwide, the moment magnitude scale (MMS) is most common, although Ms{displaystyle M_{text{s}}}M_{text{s}} is also reported frequently.


The seismic moment, Mo{displaystyle M_{o}}M_o, is proportional to the area of the rupture times the average slip that took place in the earthquake, thus it measures the physical size of the event. Mw{displaystyle M_{text{w}}}M_text{w} is derived from it empirically as a quantity without units, just a number designed to conform to the Ms{displaystyle M_{text{s}}}M_{text{s}} scale.[20] A spectral analysis is required to obtain Mo{displaystyle M_{o}}M_o, whereas the other magnitudes are derived from a simple measurement of the amplitude of a specifically defined wave.


All scales, except Mw{displaystyle M_{text{w}}}M_text{w}, saturate for large earthquakes, meaning they are based on the amplitudes of waves which have a wavelength shorter than the rupture length of the earthquakes. These short waves (high frequency waves) are too short a yardstick to measure the extent of the event. The resulting effective upper limit of measurement for ML{displaystyle M_{L}}M_L is about 7 and about 8.5[21] for Ms{displaystyle M_{text{s}}}M_{text{s}}.[22]


New techniques to avoid the saturation problem and to measure magnitudes rapidly for very large earthquakes are being developed. One of these is based on the long period P-wave;[23] the other is based on a recently discovered channel wave.[24]


The energy release of an earthquake,[25] which closely correlates to its destructive power, scales with the ​3⁄2 power of the shaking amplitude. Thus, a difference in magnitude of 1.0 is equivalent to a factor of 31.6 (=(101.0)(3/2){displaystyle =({10^{1.0}})^{(3/2)}}=({10^{1.0}})^{(3/2)}) in the energy released; a difference in magnitude of 2.0 is equivalent to a factor of 1000 (=(102.0)(3/2){displaystyle =({10^{2.0}})^{(3/2)}}=({10^{2.0}})^{(3/2)}) in the energy released.[26] The elastic energy radiated is best derived from an integration of the radiated spectrum, but an estimate can be based on mb{displaystyle m_{text{b}}}m_text{b} because most energy is carried by the high frequency waves.



Richter magnitudes



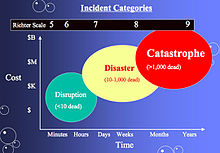
Earthquake severity.jpg


The Richter magnitude of an earthquake is determined from the logarithm of the amplitude of waves recorded by seismographs (adjustments are included to compensate for the variation in the distance between the various seismographs and the epicenter of the earthquake). The original formula is:[27]


ML=log10⁡A−log10⁡A0(δ)=log10⁡[A/A0(δ)], {displaystyle M_{mathrm {L} }=log _{10}A-log _{10}A_{mathrm {0} }(delta )=log _{10}[A/A_{mathrm {0} }(delta )], }M_mathrm{L} = log_{10} A - log_{10} A_mathrm{0}(delta) = log_{10} [A / A_mathrm{0}(delta)],

where A is the maximum excursion of the Wood-Anderson seismograph, the empirical function A0 depends only on the epicentral distance of the station, δ{displaystyle delta }delta . In practice, readings from all observing stations are averaged after adjustment with station-specific corrections to obtain the ML{displaystyle M_{text{L}}}M_text{L} value.


Because of the logarithmic basis of the scale, each whole number increase in magnitude represents a tenfold increase in measured amplitude; in terms of energy, each whole number increase corresponds to an increase of about 31.6 times the amount of energy released, and each increase of 0.2 corresponds to approximately a doubling of the energy released.


Events with magnitudes greater than 4.5 are strong enough to be recorded by a seismograph anywhere in the world, so long as its sensors are not located in the earthquake's shadow.[citation needed]


The following describes the typical effects of earthquakes of various magnitudes near the epicenter. The values are typical only. They should be taken with extreme caution, since intensity and thus ground effects depend not only on the magnitude, but also on the distance to the epicenter, the depth of the earthquake's focus beneath the epicenter, the location of the epicenter and geological conditions (certain terrains can amplify seismic signals).





































































Magnitude
 Description
Mercalli intensity
 Average earthquake effects
 Average frequency of occurrence (estimated)
1.0–1.9
Micro
I
 Microearthquakes, not felt, or felt rarely. Recorded by seismographs.[28]
 Continual/several million per year
2.0–2.9
 Minor
I to II
 Felt slightly by some people. No damage to buildings.
 Over one million per year
3.0–3.9
III to IV
 Often felt by people, but very rarely causes damage. Shaking of indoor objects can be noticeable.
 Over 100,000 per year
4.0–4.9
 Light
IV to VI
 Noticeable shaking of indoor objects and rattling noises. Felt by most people in the affected area. Slightly felt outside. Generally causes none to minimal damage. Moderate to significant damage very unlikely. Some objects may fall off shelves or be knocked over.
 10,000 to 15,000 per year
5.0–5.9
 Moderate
VI to VII
 Can cause damage of varying severity to poorly constructed buildings. At most, none to slight damage to all other buildings. Felt by everyone.
 1,000 to 1,500 per year
6.0–6.9
 Strong
VIII to X
 Damage to a moderate number of well-built structures in populated areas. Earthquake-resistant structures survive with slight to moderate damage. Poorly designed structures receive moderate to severe damage. Felt in wider areas; up to hundreds of miles/kilometers from the epicenter. Strong to violent shaking in epicentral area.
 100 to 150 per year
7.0–7.9
 Major
X or greater[29]
 Causes damage to most buildings, some to partially or completely collapse or receive severe damage. Well-designed structures are likely to receive damage. Felt across great distances with major damage mostly limited to 250 km from epicenter.
 10 to 20 per year
8.0–8.9
 Great
 Major damage to buildings, structures likely to be destroyed. Will cause moderate to heavy damage to sturdy or earthquake-resistant buildings. Damaging in large areas. Felt in extremely large regions.
 One per year
9.0 and greater
 At or near total destruction – severe damage or collapse to all buildings. Heavy damage and shaking extends to distant locations. Permanent changes in ground topography.
 One per 10 to 50 years

(Based on U.S. Geological Survey documents.)[30]


The intensity and death toll depend on several factors (earthquake depth, epicenter location, population density, to name a few) and can vary widely.


Minor earthquakes occur every day and hour. On the other hand, great earthquakes occur once a year, on average. The largest recorded earthquake was the Great Chilean earthquake of May 22, 1960, which had a magnitude of 9.5 on the moment magnitude scale.[31] The larger the magnitude, the less frequently the earthquake happens.


Seismologist Susan Hough has suggested that 10 may represent a very approximate upper limit, as the effect if the largest known continuous belt of faults ruptured together (along the Pacific coast of the Americas).[32]



Magnitude empirical formulae


These formulae for Richter magnitude ML{displaystyle textstyle M_{mathrm {L} }}{displaystyle textstyle M_{mathrm {L} }} are alternatives to using Richter correlation tables based on Richter standard seismic event (ML=0{displaystyle M_{mathrm {L} }=0}{displaystyle M_{mathrm {L} }=0}, A=0.001mm{displaystyle A=0.001mm}{displaystyle A=0.001mm}, D=100km{displaystyle D=100km}{displaystyle D=100km}). Below, Δ{displaystyle textstyle Delta }textstyle Delta is the epicentral distance (in kilometers unless otherwise specified).


The Lillie empirical formula:


ML=log10⁡A−2.48+2.76log10⁡Δ,{displaystyle M_{mathrm {L} }=log _{10}A-2.48+2.76log _{10}Delta ,}{displaystyle M_{mathrm {L} }=log _{10}A-2.48+2.76log _{10}Delta ,}

Where A{displaystyle A}A is the amplitude (maximum ground displacement) of the P-wave, in micrometers, measured at 0.8 Hz.


For distances D{displaystyle D}D less than 200 km,


ML=log10⁡A+1.6log10⁡D−0.15,{displaystyle M_{mathrm {L} }=log _{10}A+1.6log _{10}D-0.15,}{displaystyle M_{mathrm {L} }=log _{10}A+1.6log _{10}D-0.15,}

and for distances between 200 km and 600 km,


ML=log10⁡A+3.0log10⁡D−3.38,{displaystyle M_{mathrm {L} }=log _{10}A+3.0log _{10}D-3.38,}{displaystyle M_{mathrm {L} }=log _{10}A+3.0log _{10}D-3.38,}

where A{displaystyle A}A is seismograph signal amplitude in mm and D{displaystyle D}D is in km.


The Bisztricsany (1958) empirical formula for epicentral distances between 4˚ to 160˚:[33]


ML=2.92+2.25log10⁡(τ)−0.001Δ∘,{displaystyle M_{mathrm {L} }=2.92+2.25log _{10}(tau )-0.001Delta ^{circ },}{displaystyle M_{mathrm {L} }=2.92+2.25log _{10}(tau )-0.001Delta ^{circ },}

Where τ{displaystyle tau }tau is the duration of the surface wave in seconds, and Δ{displaystyle Delta }Delta is in degrees. ML{displaystyle M_{mathrm {L} }}M_{mathrm {L} } is mainly between 5 and 8.


The Tsumura empirical formula:[33]


ML=−2.53+2.85log10⁡(F−P)+0.0014Δ∘{displaystyle M_{mathrm {L} }=-2.53+2.85log _{10}(F-P)+0.0014Delta ^{circ }}M_mathrm{L} = -2.53 + 2.85 log_{10} (F-P) + 0.0014 Delta^{circ}

Where F−P{displaystyle F-P}F-P is the total duration of oscillation in seconds. ML{displaystyle M_{mathrm {L} }}M_{mathrm {L} } is mainly between 3 and 5.


The Tsuboi, University of Tokyo, empirical formula:


ML=log10⁡A+1.73log10⁡Δ−0.83{displaystyle M_{mathrm {L} }=log _{10}A+1.73log _{10}Delta -0.83}M_mathrm{L} = log_{10}A + 1.73log_{10}Delta - 0.83

Where A{displaystyle A}A is the amplitude in micrometers.



See also





  • 1935 in science

  • Moment magnitude scale


  • Rohn Emergency Scale for measuring the magnitude (intensity) of any emergency

  • Seismic intensity scales

  • Seismic magnitude scales

  • Timeline of United States inventions (1890–1945)#Great Depression and World War II (1929–1945)




Notes





  1. ^ Bolt 1993, p. 47.


  2. ^ Hough 2007;


  3. ^ Hough 2007, p. 57.


  4. ^ Hough 2007, pp. 57, 116.


  5. ^ Richter 1935, p. 2.


  6. ^ Richter 1935, pp. 1–5.


  7. ^ Richter 1935, pp. 2–3.


  8. ^ [pending]


  9. ^ Richter 1935, p. 14: Gutenberg & Richter 1936, p. 183.


  10. ^ Richter 1935, p. 5. See also Hutton & Boore 1987, p. 1; Chung & Bernreuter 1980, p. 10.


  11. ^ Richter 1935, p. 6, Table I.


  12. ^ Richter 1935, p. 32.


  13. ^ Chung & Bernreuter 1980, p. 5.


  14. ^ Richter 1935, p. 1. His article is titled: "An Instrumental Earthquake Magnitude Scale".


  15. ^ Hough 2007, pp. 123–124.


  16. ^ Gutenberg & Richter 1956b, p. 30.


  17. ^ "Explanation of Bulletin Listings, USGS"..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output q{quotes:"""""""'""'"}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-limited a,.mw-parser-output .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}


  18. ^ Richter 1935.


  19. ^ Richter, C.F., "Elementary Seismology", ed, Vol., W. H. Freeman and Co., San Francisco, 1956.


  20. ^ Hanks, T. C. and H. Kanamori, 1979, "Moment magnitude scale", Journal of Geophysical Research, 84, B5, 2348.


  21. ^ Woo, Wang-chun (September 2012). "On Earthquake Magnitudes". Hong Kong Observatory. Retrieved 18 December 2013.


  22. ^ "Richter scale". Glossary. USGS. March 31, 2010.


  23. ^ Di Giacomo, D., Parolai, S., Saul, J., Grosser, H., Bormann, P., Wang, R. & Zschau, J., 2008. "Rapid determination of the energy magnitude Me," in European Seismological Commission 31st General Assembly, Hersonissos.


  24. ^ Rivera, L. & Kanamori, H., 2008. "Rapid source inversion of W phase for tsunami warning," in European Geophysical Union General Assembly, pp. A-06228, Vienna.


  25. ^ Marius Vassiliou and Hiroo Kanamori (1982): "The Energy Release in Earthquakes," Bull. Seismol. Soc. Am. 72, 371–387.


  26. ^ William Spence, Stuart A. Sipkin, and George L. Choy (1989). "Measuring the Size of an Earthquake". Earthquakes and Volcanoes. 21 (1).CS1 maint: Uses authors parameter (link)


  27. ^ Ellsworth, William L. (1991). "The Richter Scale ML{displaystyle M_{text{L}}}M_text{L}, from The San Andreas Fault System, California (Professional Paper 1515)". USGS: c6, p177. Retrieved 2008-09-14.


  28. ^ This is what Richter wrote in his Elementary Seismology (1958), an opinion copiously reproduced afterwards in Earth's science primers. Recent evidence shows that earthquakes with negative magnitudes (down to −0.7) can also be felt in exceptional cases, especially when the focus is very shallow (a few hundred metres). See: Thouvenot, F.; Bouchon, M. (2008). "What is the lowest magnitude threshold at which an earthquake can be felt or heard, or objects thrown into the air?," in Fréchet, J., Meghraoui, M. & Stucchi, M. (eds), Modern Approaches in Solid Earth Sciences (vol. 2), Historical Seismology: Interdisciplinary Studies of Past and Recent Earthquakes, Springer, Dordrecht, 313–326.


  29. ^ "Anchorage, Alaska (AK) profile: population, maps, real estate, averages, homes, statistics, relocation, travel, jobs, hospitals, schools, crime, moving, houses, news". City-Data.com. Retrieved 2012-10-12.


  30. ^ "Earthquake Facts and Statistics". United States Geological Survey. November 29, 2012. Archived from the original on May 24, 2010. Retrieved December 18, 2013.


  31. ^ "Largest Earthquakes in the World Since 1900". November 30, 2012. Archived from the original on October 7, 2009. Retrieved December 18, 2013.


  32. ^ Silver, Nate (2013). The signal and the noise : the art and science of prediction. London: Penguin. ISBN 9780141975658.


  33. ^ ab Al-Arifi, Nassir S.; Al-Humidan, Saad (July 2012). "Local and regional earthquake magnitude calibration of Tabuk analog sub-network, Northwest of Saudi Arabia". Journal of King Saud University – Science. 24 (3): 257–263. doi:10.1016/j.jksus.2011.04.001.




Sources


.mw-parser-output .refbegin{font-size:90%;margin-bottom:0.5em}.mw-parser-output .refbegin-hanging-indents>ul{list-style-type:none;margin-left:0}.mw-parser-output .refbegin-hanging-indents>ul>li,.mw-parser-output .refbegin-hanging-indents>dl>dd{margin-left:0;padding-left:3.2em;text-indent:-3.2em;list-style:none}.mw-parser-output .refbegin-100{font-size:100%}


  • Bolt, B. A. (1993), Earthquakes and geological discovery, Scientific American Library, ISBN 0-7167-5040-6.


  • Boore, D. M. (September 1989), "The Richter scale: its development and use for determining earthquake source parameter" (PDF), Tectonophysics, 166 (1–3): 1–14


  • Chung, D. H.; Bernreuter, D. L. (1980), Regional Relationships Among Earthquake Magnitude Scales., NUREG/CR-1457.


  • Gutenberg, B.; Richter, C. F. (21 February 1936), "Discussion: Magnitude and energy of earthquakes" (PDF), Science, 83 (2147): 183–185, doi:10.1126/science.83.2147.183.


  • Gutenberg, B.; Richter, C. F. (1956b), "Earthquake magnitude, intensity, energy, and acceleration (Second Paper)", Bulletin of the Seismological Society of America, 46 (2): 105–145.


  • Hough, S. E. (2007), Richter's scale: measure of an earthquake, measure of a man, Princeton University Press, ISBN 978-0-691-12807-8.


  • Hutton, L. K.; Boore, David M. (December 1987), "The ML scale in Southern California" (PDF), Nature, 271: 411–414, doi:10.1038/271411a0.


  • Richter, C. F. (January 1935), "An Instrumental Earthquake Magnitude Scale" (PDF), Bulletin of the Seismological Society of America, 25 (1): 1–32.



External links




  • Richter scale (seismology) at Encyclopædia Britannica


  • Seismic Monitor – IRIS Consortium


  • USGS Earthquake Magnitude Policy (implemented on January 18, 2002) – USGS


  • Perspective: a graphical comparison of earthquake energy release – Pacific Tsunami Warning Center










-

Popular posts from this blog

Eastern Orthodox Church

Image
Not to be confused with Oriental Orthodoxy, Eastern Christianity, or Eastern Catholic Churches. "Eastern Orthodoxy", "Orthodox Church", "Orthodox Catholic Church", and "Orthodox Christian Church" redirect here. For other uses, see Orthodox (disambiguation). This article may be too long to read and navigate comfortably . The readable prose size is 132 kilobytes. Please consider splitting content into sub-articles, condensing it, or adding or removing subheadings. ( January 2018 ) Part of a series on the Eastern Orthodox Church Mosaic of Christ Pantocrator, Hagia Sophia Overview Structure Theology (History of theology) Liturgy Church history Holy Mysteries View of salvation View of Mary View of icons Background Crucifixion / Resurrection / Ascension of Jesus Christianity Christian Church Apostolic succession Four Marks of the Church Orthodoxy Organization Autocephaly Patriarchate ...
Read more

Zagreb

Image
This article is about the Croatian capital city. For other uses, see Zagreb (disambiguation). City in City of Zagreb, Croatia Zagreb City Grad Zagreb City of Zagreb Clockwise, from top: St. Mark's Square, Croatian State Archives, Zagreb Tram, Art Pavilion, Cibona & HOTO towers and Croatian National Theatre. Flag Coat of arms Zagreb Location of Zagreb in Croatia Show map of Croatia Zagreb Zagreb (Europe) Show map of Europe Coordinates: 45°49′N 15°59′E  /  45.817°N 15.983°E  / 45.817; 15.983 Coordinates: 45°49′N 15°59′E  /  45.817°N 15.983°E  / 45.817; 15.983 Country   Croatia County City of Zagreb RC diocese 1094 Free royal city 1242 Unified 1850 Subdivisions 17 city districts 218 local committees (70 settlements) Government  • Type Mayor-Council  • Mayor Milan Bandić (BM 365)  • City Assembly 51 members BM 365, ZL, NS-R (14) SDP, GLAS, HNS, HSS, NH-PS (13) ...
Read more

Understanding the information contained in the Deep Space Network XML data?

Image
up vote 1 down vote favorite NASA's Deep Space Network activity can be viewed conveniently at https://eyes.nasa.gov/dsn/dsn.html but if you would like data in a more raw XML form, it can be accessed as described in this answer Below is a small Python script that reads the XML into a list of dictionaries, and saves it to disk as a JSON. The dictionaries are organized at the higher level by dish, then by spacecraft per dish. Question: What are the most-likely meanings of all the data field contained in the Deep Space Network XML data? This is the example url from the other answer, used in the script below: https://eyes.nasa.gov/dsn/data/1365107113.xml def dictify(r,root=True): # https://stackoverflow.com/questions/2148119/how-to-convert-an-xml-string-to-a-dictionary-in-python/30923963#30923963 if root: ret...
Read more